Research

Research Interests

My research efforts focus on understanding processes in complex soft materials and biological systems. In particular, I am interested in pattern and shape formation in multi-components solid and liquid membranes, self-assembly of complex, nanocomposite materials at nano-scales and cell and tissue mechanics.
I have an extensive experience with molecular dynamics and Monte Carlo methods and scientific software development. Part of my research is devoted to the development of new simulation techniques and their implementation on specialized, high performance hardware, like modern graphics cards (scientific GPU programming).

Research Highlights

Active systems in curved geometries

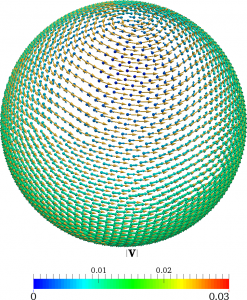J_1.00_v0_0.01_k_1.0_vel_dirHere we show that coupling to curvature has profound effects on collective motion in active systems, leading to patterns not observed in flat space. Biological examples of such active motion in curved environments are numerous: curvature and tissue folding are crucial during gastrulation, epithelial and endothelial cells move on constantly growing, curved crypts and vili in the gut, and the mammalian corneal epithelium grows in a steady-state vortex pattern. On the physics side, droplets coated with actively driven microtubule bundles show active nematic patterns. We study a model of self-propelled particles with polar alignment on a sphere. Hallmarks of these motion patterns are a polar vortex and a circulating band arising due to the incompatibility between spherical topology and uniform motion – a consequence of the hairy ball theorem. We present analytical results showing that frustration due to curvature leads to stable elastic distortions storing energy in the band.

Defect dynamics in active nematics

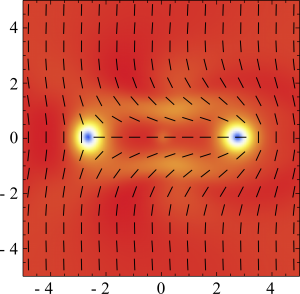active_anihTopological defects are distinctive signatures of liquid crystals. They profoundly affect the viscoelastic behavior of the fluid by constraining the orientational structure in a way that inevitably requires global changes not achievable with any set of local deformations. In active nematic liquid crystals topological defects not only dictate the global structure of the director, but also act as local sources of motion, behaving as self-propelled particles. In this article we present a detailed analytical and numerical study of the mechanics of topological defects in active nematic liquid crystals.

  • L. Giomi, M. J. Bowick, P. Mishra, R. Sknepnek, M. C. Marchetti
    Defect dynamics in active nematics
    Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 372.2029: 20130365 (2014), arXiv:1403.5254

Shapes of adherent cells on patterned substrates

We investigate a continuustress_CROSSshape_SIGMA_10_KAPPA_40m mechanical model for an adherent cell on two dimensional adhesive micropatterned substrates. The cell is modeled as an isotropic and homogeneous elastic material subject to uniform internal contractile stresses. The build-up of tension from cortical actin bundles at the cell periphery is incorporated by introducing an energy cost for bending of the cell boundary, resulting to a resistance to changes in local curvature. Integrin-based adhesions are modeled as harmonic springs, that pin the cell to adhesive patches of a predefined geometry. Using Monte Carlo simulations and analytical techniques we investigate the competing effects of bulk contractility and cortical bending rigidity in regulating cell shapes on non-adherent regions. We show that the crossover from convex to concave cell edges is controlled by the interplay between contractile stresses and boundary bending rigidity. In particular, the cell boundary becomes concave beyond a critical value of the contractile stress that is proportional to the cortical bending rigidity. Furthermore, the intracellular stresses are found largely concentrated at the concave edge of the cell. The model can be used to generate a cell-shape phase diagram for each specific adhesion geometry.

Modeling of endocytosis in yeast

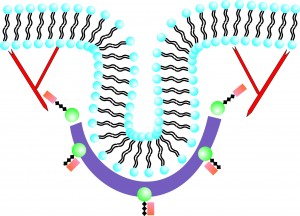model_clatrin_dimple_step_3During endocytosis, the cell membrane deforms to surround extracellular material and draw it into the cell. Experiments on clathrin-mediated endocytosis in yeast all agree that (i) actin polymerizes into a network of filaments exerting active forces on the membrane to deform it and (ii) the large scale membrane deformation is tubular in shape. Three competing ideas remain as to precisely how the actin filament network organizes itself to drive the deformation. To begin to address this issue, we use variational approaches and numerical simulations to analyze a meso-scale model of clathrin-mediated endocytosis in yeast. The meso-scale model breaks up the invagination process into three stages: (i) the initiation stage, where clathrin interacts with the membrane, (ii) the elongation stage, where the membrane is then pulled and/or squeezed via polymerizing actin filaments, followed by a (iii) final pinch-off stage. Our results suggest that the pinch-off mechanism is assisted by a pearling-like instability. In addition, we potentially rule out two of the three competing models for the organization of the actin filament network during the elongation stage. These two models could possibly be important in the pinch-off stage, however, where actin polymerization helps break off the vesicle. Implications and comparisons with earlier modeling of clathrin-mediated endocytosis in yeast is discussed.

Blebbing in nuclear lamina

Much of the structural stability of the nucleus comes from meshworks of intermediate filament proteins known as lamins forming the inner layer of the nuclear envelope called the nuclear lamina. These lamin meshworks additionally play a role in gene expression. Abnormalities in nuclear shape are associated with a variety of pathologies, including some forms of cancer and Hutchinson-Gilford Progeria Syndrome, and often include protruding structures termed “nuclear blebs.” These nuclear blebs are thought to be related to pathological gene expression, however, little is known about how and why blebs form. We have developed a minimal continuum elastic model of a lamin meshwork that we employ to investigate which aspects of the meshwork could be responsible for bleb formation. Mammalian lamin meshworks consist of two types of lamin proteins, A-type and B-type, and it has been reported that nuclear blebs are enriched in A-type lamins. Our model treats each lamin type separately, and can thus assign them different properties. Nuclear blebs have been reported to be located in regions where the fibers in the lamin meshwork have a greater separation, and we find that this is an essential characteristic for generating nuclear blebs. The model produces structures with comparable morphologies and distributions of lamin types as real, pathological nuclei. Thus, preventing this opening of the meshwork could be a route to prevent bleb formation, which could be used as a potential therapy for the pathologies associated with nuclear blebs.

Thin sheets on negative curvature surfaces

Gauss’s Theorema Egregium provides an intimate connection between the metric and the Gaussian curvature of a surface. A mismatch in topology between a sphere and a plane prevents smooth covering of a sphere with a flat sheet. As a result wrinkles and folds arise. These are narrow regions of highly focused deformation. If a thin sheet is adhered to a substrate with a negative Gaussian curvature it will experience stress due to the curvature-driven change of its metric. In the inextensible limit any changes of metric are not possible and the sheet will relieve the stress by locally deforming via wrinkles or folds. We analyze the consequences of such geometric frustration using analytic arguments and numerical simulations. Both concentric wrinkles and eye-like folds are shown to be compatible with negative curvatures. Which pattern will be realized depends on the curvature of the substrate. We discuss both types of folding patterns and determine the phase diagram governing their appearance.

DNA-driven assembly of nanoparticles

Over past decade there has been a tremendous development in the field of guided assembly of nano-composite materials. DNA molecules have been extensively used in this process for their controllable selectivity in binding and their biocompatibility. With this bottom-up approach, spherical nucleic acid gold nanoparticle conjugates can be used as artificial “atoms”, where the oligonucleotides connecting the nanoparticles are “chemical bonds” that can be used to create novel one-, two-, and three-dimensional superlattices. We use molecular dynamics simulations to study the crystallization of spherical nucleic-acid (SNA) gold nanoparticle conjugates, guided by sequence-specific DNA hybridization events. Binary mixtures of SNA gold nanoparticle conjugates (inorganic core diameter in the 8–15 nm range) are shown to assemble into BCC, CsCl, AlB2, and Cr3Si crystalline structures, depending upon particle stoichiometry, number of immobilized strands of DNA per particle, DNA sequence length, and hydrodynamic size ratio of the conjugates involved in crystallization. These data have been used to construct phase diagrams that are in excellent agreement with experimental data from wet-laboratory studies.

Curvature-driven shapes of liquid vesicles

We study closed liquid membranes that segregate into three phases due to differences in the chemical and physical properties of its components. The shape and in-plane membrane arrangement of the phases are coupled through phase-specific bending energies and line tensions. We use simulated annealing Monte Carlo simulations to find low-energy structures, allowing both phase arrangement and membrane shape to relax. The three-phase system is the simplest one in which there are multiple interface pairs, allowing us to analyze interfacial preferences and pairwise distinct line tensions. We observe the system’s preference for interface pairs that maximize differences in spontaneous curvature. From a pattern selection perspective, this acts as an effective attraction between phases of most disparate spontaneous curvature. We show that this effective attraction is robust enough to persist even when the interface between these phases is the most penalized by line tension. This effect is driven by geometry and not by any explicit component-component interaction.

Coarse-grained simulations of charged lipid bilayers

By combining Molecular Dynamics simulations and analytical arguments we investigate the elastic properties of charged lipid bilayers. We show that electrostatic interactions between the head groups can lead to solidification of the lipid bilayer that would otherwise be in a liquid state if the charges were absent. All elastic parameters of the bilayer such as the bending rigidity and the two-dimensional bulk modulus and Young’s modulus are found to depend on the values of the charges assigned to the lipid head groups. To extract Young’s modulus and bulk modulus we fit the Molecular Dynamics data to a standard elastic model for lipid bilayers. Moreover, we analytically obtain the dependence of the Young’s modulus on the relative strengths of electrostatic and van der Waals interactions in the zero temperature limit.

Shapes of multicomponent elastic membranes

Membranes are an essential part of all biological systems. Most notable examples include the cell membrane, a complex barrier that separates interior of a cell from its environment, the nuclear envelope, a thin layer encompassing nuclei of all eukaryotic cells, the mitochondrial membrane, etc. At physiological conditions, lipid membranes are typically in a liquid state, that is, lipid molecules are mobile and diffuse within the bilayer. Such membrane cannot sustain a shear deformation. However, if the membrane is cooled below gelation temperature or cross linked via suitable polymerization technique, it crystalizes into an essentially two-dimensional solid. Resistance to shear results in unique physical properties, central to a number of biological processes and of potential importance for nano-technology.
Shape of a crystalline vesicle is primarily determined by the interplay of two parameters, bending rigidity, i.e., resistance of the membrane to bend, and the Young modulus, i.e., its resistance to stretch. In the regime of strong bending rigidity and low Young modulus a homogeneous vesicle will be spherical, while for large Young modulii and low bending, the vesicle will buckle into an icosahedral shape. Biological membranes are rarely homogeneous and are rather built of components with very different elastic properties. We study the shape of vesicles made of two different components with very different elastic properties. Depending on the relative concentration of two components and the strength of line tension between them, we find a very rich set of shapes, very different from spheres and icosahedra observed in single-component systems.

Charge-driven collapse of nano-cages

Long-range nature of electrostatic forces can have profound effects on the shape and properties of nano-size elastic containers, like nanocages. Due to their small size, electrostatic interaction is strong over distances comparable to the cage radius and can lead to drastic changes of the shape, including the total collapse of the structure. Using Monte Carlo simulations, we demonstrate that small charged nanocages can undergo reversible changes of shapes by modifying the ionic conditions including salt concentration, pH, and dielectric permittivity of the medium. We analyze structures with various charge stoichiometric ratios. At zero or low charge densities, the shape of the cage is determined by its elastic properties, and the surface charge pattern is dictated by the globally fixed geometry. As the charge density per molecule increases, the shape is strongly affected by the electrostatic forces. In this regime, the shape of the nanocage is controlled by the charge distribution.

Numerical simulations on the GPUs

Ever-growing demand for realistic video games triggered a rapid development of highly sophisticated, inexpensive graphics cards. These devices are designed to perform an enormous amount of computations and easily reach floating point speeds of 1TFLOPS (1012 floating point operations per second). Recently, this computational power has become available for scientific computations. Most notable example is molecular dynamics, for which GPU implementations have been reported with speedups in excess of 100 times compared to the standard CPU codes. A highly parallel architecture of modern graphics processors requires existing methods to be redesigned and new algorithms to be developed in order to fully harvest the computational power of the device.
We have recently implemented in the HOOMD Blue graphics card molecular dynamics package a long-range electrostatic interaction method based on the orientation-averaged Ewald sum scheme, introduced by Yakub and Ronchi. Our implementation reaches a speedup of up to 80 times compared to an optimized CPU version of the traditional Ewald sum available in commonly used packages, like LAMMPS. Thermodynamic and structural properties of monovalent and divalent hydrated salts in bulk are calculated for a wide range of ionic concentrations. An excellent agreement between the two methods was found at the level of electrostatic energy, heat capacity, radial distribution functions, and integrated charge of the electrolytes.

Binding of Aniline Ligands and CdSe Quantum Dots

Using 1H NMR spectroscopy we measured the equilibrium constants for the solution-phase binding of two para-substituted aniline molecules (R-An), p-methoxyaniline (MeO-An) and p-bromoaniline (Br-An), to colloidal 4.1-nm CdSe quantum dots (QDs). Changes in the chemical shifts of the aromatic protons located ortho to the amine group on R-An were used to construct a binding isotherm for each R-An/QD system. These isotherms fit to a Langmuir function to yield Ka, the equilibrium constant for binding of the R-An ligands to the QDs; Ka ≈ 150 M-1 and Gads ≈ -19 kJ/mol for both R = MeO and R = Br. 31P NMR indicated that the native octylphosphonate ligands (OPA), which, by inductively-coupled plasma atomic emission spectroscopy cover 90% of the QD surface, are not displaced upon binding of R-An. The MeOAn ligand quenches the photoluminescence of the QDs at much lower concentrations than does Br-An; the observation, therefore, that Ka,MeO-An ≈ Ka,Br-An shows that this difference in quenching efficiencies is due solely to differences in the nature of the electronic interactions of the bound R-An with the excitonic state of the QD.
Without any attraction,the native OPA ligands would tend to maximize their entropy and form a uniform, approximately 1.5-nm thick brush-like layer. In order to reach the QD surface, ligands have to diffuse through the OPA coating, so their ability to bind is suppressed. As the hydrophobicity of the OPA ligands is increased, OPA chains cluster into bundles. This process involves a loss of entropy that is compensated by the enthalpic stabilization gained through a reduction of contact with the solvent. Regions between separate bundles open up, revealing surface sites that are now accessible to the R-An molecules.

Nanoparticle assembly via functionalized triblocks

Triblock coplymers are made by joing polymers of two different types in a structure AnBmAn, where n and m are degrees of polymerization of polymers A and B respectively. Triblocks can be modified by covalently attaching functional groups with affinity for nanoparticles. By controlling the affinity for nanoparticles functiolaized triblock copolymers can be used to control self-assembly of nanoparticles into a number of two and three dimensional ordered structures. Using coarse grained molecular dynamics simulations we show that under reasonable assumptions about the coplymer/nanoparticle interaction one could realize a large number of stable ordered structures, including unusual square and bicontinuous triply periodic (gyroid) orderings. Our simulations prove that in principal functionalized block copolymers can provide a simple and robust tool to control self-assembly at nanometer length scales.

Older project in hard condensed matter theory

Multiband superconductivity

Recent discovery of superconductivity in FeAs based compounds has attracted a lot of attention due to its rather large transition temperature. Although possible, it is unlikely that the superconducting pairing is caused by typical electron-lattice interaction responsible for the conventional superconductivity. Observation of antiferromagnetic ordering in undopped systems at ambient pressure suggest that spin fluctuations might be the primary mechanism of superconductivity in these compounds. The glue that keeps Cooper pairs together is provided by bosonic collective paramagnon excitations of the electron liquid, a role played by phonons in the conventional superconductivity. Nuclear magnetic resonace experiments indicate existence of nodes in the superconducting gap, while angle resolved photoemission spectroscopy find nodeless, weakly unisotropic gap at the Fermi surface. This suggests that there are multiple gap values originating in different electron bands. Using many-body fluctuation exchange (FLEX) calulation we determine the anisotropy of the spin fluctuation induced pairing gap on the Fermi surface of the FeAs based superconductors as function of the exchange and Hund’s coupling J.

Universality of Mott transitions

Band theory of solids predicts that materials with a single electron per unit cell are metals. However experiments show that in general this is not the case. There are two competing energy scales, on-site Coluomb repulsion U, and kinetic energy represented by the bandwidth W. Coulomb repulsion prefers configurations with single electron site occupancy, while kinetic part prefers electrons hopping between sites. For U less that some critical value Uc, knetic term dominates and material is a metal. If the on-site Coloumb repulsion reaches the critical value, it becomes energetically unfavorable for electrons to move, and material is an insulator. This metal-insulator phase transition is known Mott transition. At sufficiently high temperatures, when no symmetry is broken, the Mott transition is characterized by paramagnetic insulating and metallic phases, whose coexistence terminates at a second-order critical point. In this work we explain in a consistent manner the set of seemingly conflicting experiments on the finite temperature Mott critical point, and demonstrate that the Mott transition is in the Ising universality class.

Leave a Reply

Your email address will not be published. Required fields are marked *