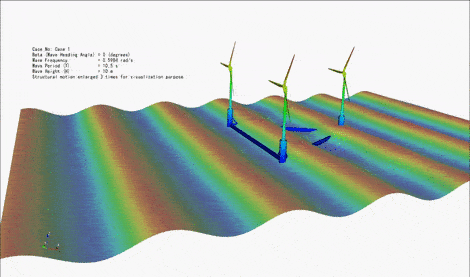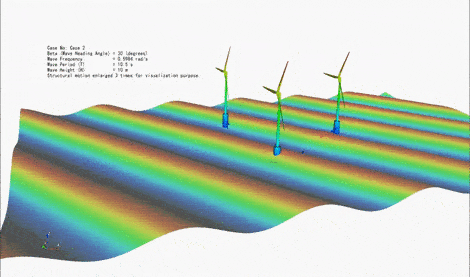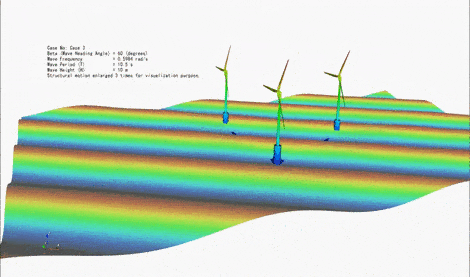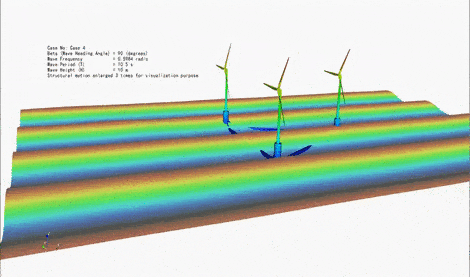
Floating Offshore Wind Turbines are typically under the action of three types of external loads, namely (i) hydrodynamic loads due to waves and current, (ii) aerodynamic loads due to wind, and (iii) restoring loads due to the mooring lines attached to the seabed. The magnitude of these loads can be comparable depending on the conditions. Hence, it is essential to consider these loads simultaneously, including the interaction between them. Responses of structure to these environmental loads include (i) translational and rotational motions of the floating body, and (ii) the elastic deformation of the floater and the turbine. We are particularly interested in the analysis of an emerging generation of floating offshore structures that host multiple wind turbines. We are developing several theoretical approaches to consider coupled wave-wind-current loads on floating structures and determine their motion and elastic (hydroelastic and aeroelastic) responses. The subject is also investigated through laboratory experiments in deep-water basin.
Wave Energy, a form of Marine Renewable Energy, is clean, highly predictable, and its seasonal availability is usually in harmony with demand. Challenging problems associated to Wave Energy Converters include their complex designs, impact of large waves on the devices at the surface, visual impacts at near-shore areas, and the device and project cost. A novel, fully submerged wave energy converter is proposed to address these common issues; concept of which is shown in the below animation. The submerged device consists of a horizontal disc that oscillates due to the wave loads. The vertical oscillations of the disk is converted into electricity by use of a direct-driven power take-off system. This device is analysed by various theoretical approaches and by conducting laboratory experiments.

In the early 1970s, Professor Albert Edward Green (Mathematical Institute of Oxford, 1912-1999) and Professor Paul Mansour Naghdi (University of Berkeley, 1924-1994) developed a general theory, based on the Theory of Directed Fluid Sheets, for propagation of waves in sheet-like bodies. In this theory, the continuum is modeled by a directed or Cosserat surface. A Cosserat surface is a 2D surface embedded in a 3D Euclidian space with deformable vectors, called directors, assigned to every point of this surface. In water waves, the directors, prescribe the distribution of the vertical velocity along the water column.
In 1984, Professor R. Cengiz Ertekin (University of Hawaii) named the system of equations for waves propagating in water of variable depth, The Green-Naghdi (GN) equations. The GN equations are categorized according to their Levels, each increasing Level corresponding to an increasing order of distribution function of the vertical velocity, and in principle to increasing level of accuracy. The GN equations satisfy the integrated form of the constitutive laws and the free-surface and sea-floor boundary conditions exactly. The general form of the theory does not require the fluid to be inviscid or the flow to be irrotational, but the fluid is assumed to be incompressible.
The following animation shows an example of propagation of nonlinear waves of the solitary and cnoidal types over a 3D ramp, solved by the GN equations.
Typically, with the price of higher computational cost, Computational Fluid Dynamics methods can be utilized in approximating the solutions to several hydrodynamic problems. For example, in the following animation, the open source computational fluid dynamics package, namely Open Field Operation And Manipulation (OpenFOAM), is used to study the interaction of a solitary wave with a bridge deck. In this example, InterFoam solver of OpenFOAM is utilized, and the Navier-Stokes equations are approximated to Euler’s equations by setting the fluid viscosity to zero (approximately). An interface capturing approach, namely Volume of Fluid (VOF) method, is implemented to determine the free surface.

The lattice Boltzmann method (LBM) is a relatively new computational method to model fluid flows by tracking collision, advection, and propagation of mesoscopic fluid particles. LBM is originated from the cellular automata combined with kinetic theory and the Boltzmann equation. The method is used to solve the explicit finite-difference scheme lattice Boltzmann equations which are second order in space and first order in time. LBM does not attempt to solve the Navier–Stokes equations directly; however, it obeys the equations.
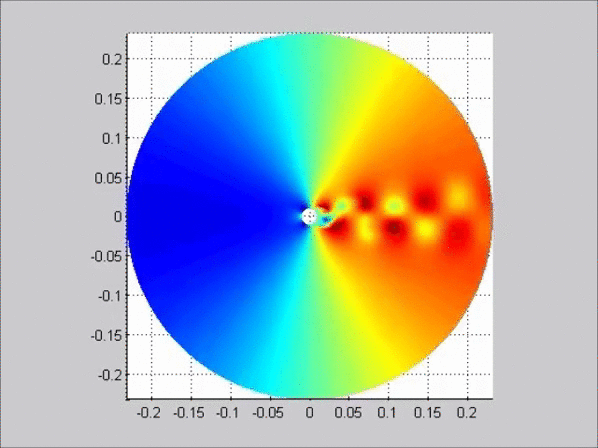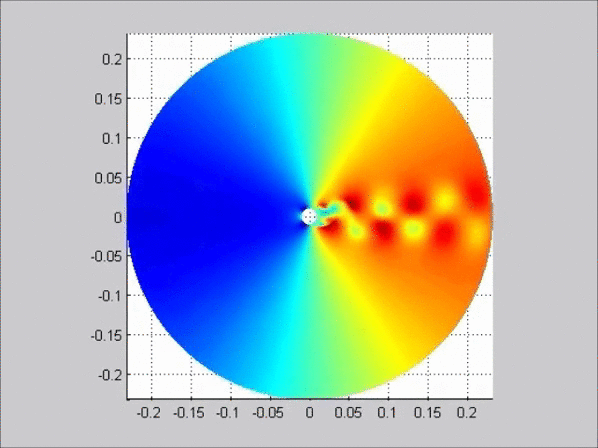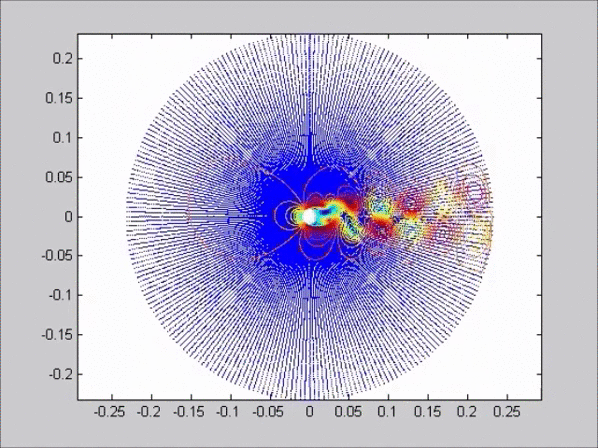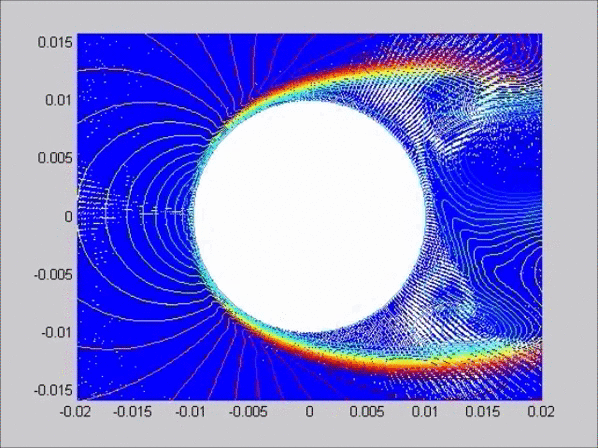
In the below examples, LBM equations are solved to study the problems of interaction of low Reynolds flows around submerged (away from the free surface) circular cylinders and ship shapes in curvilinear and rectangular coordinate systems, respectively.
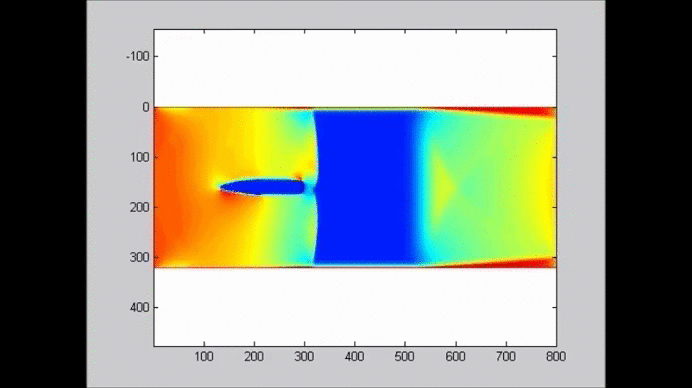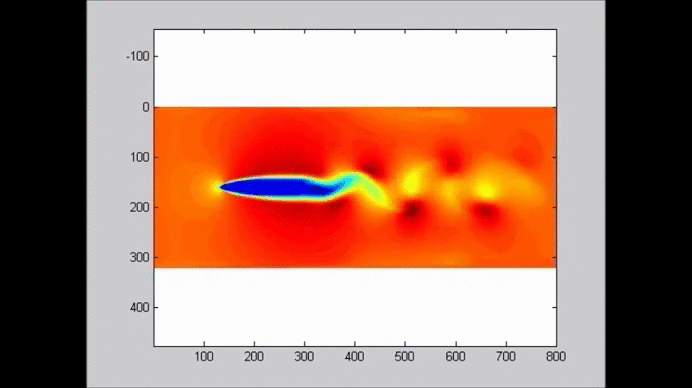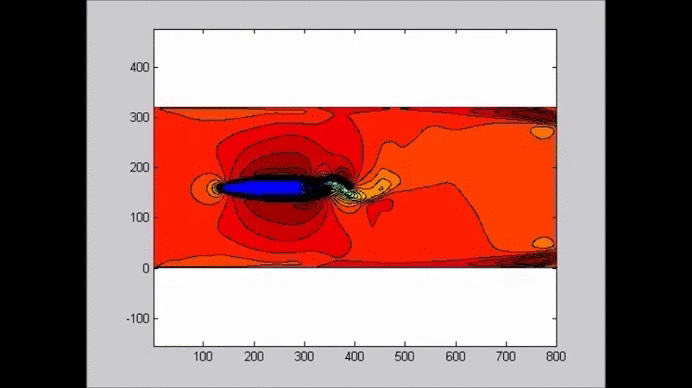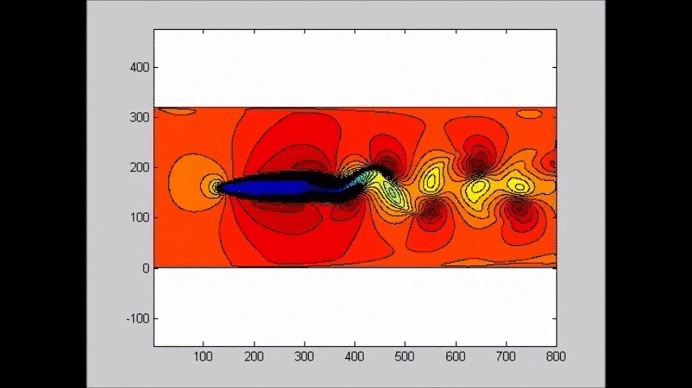
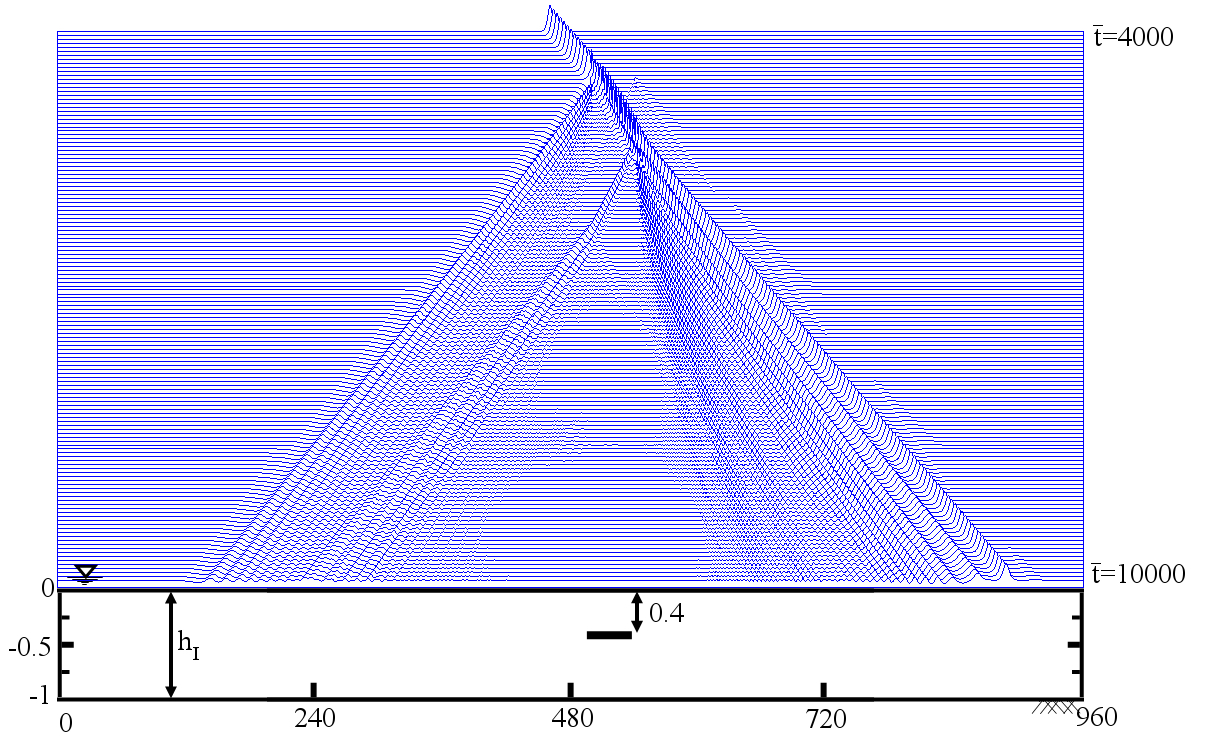
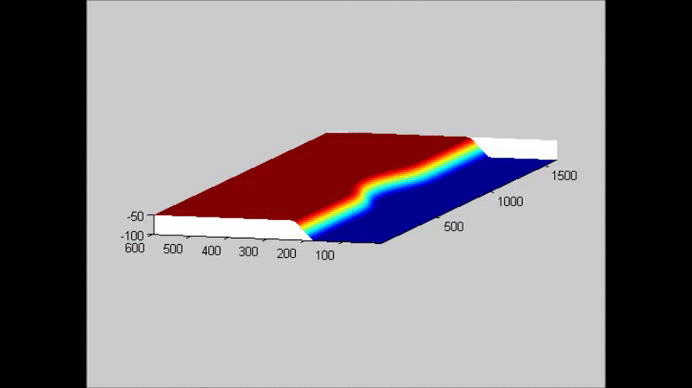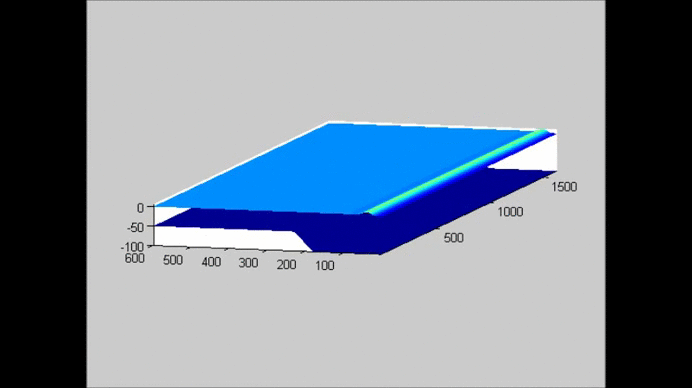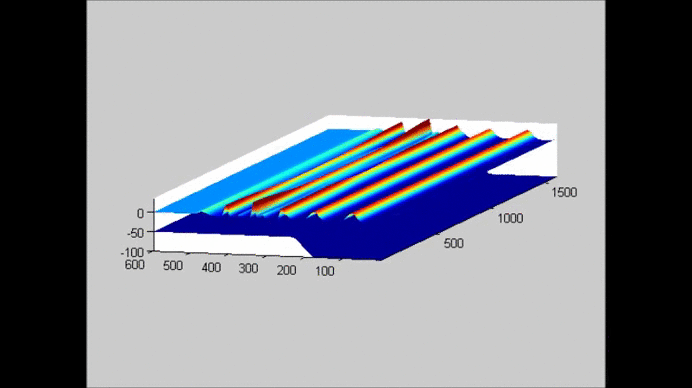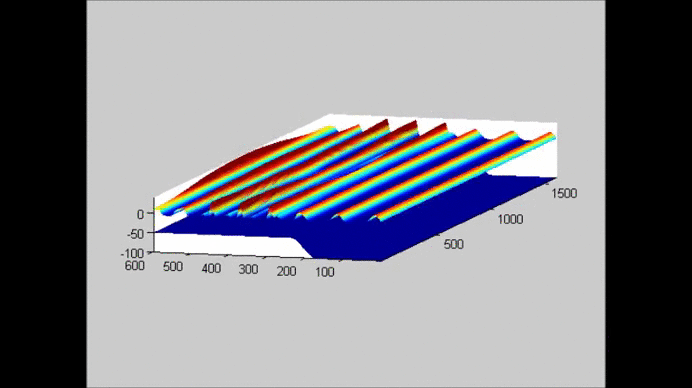
The following figure shows an example of the evolution of a solitary wave propagating over a submerged plate studied by solving the Level I Green-Naghdi equations. The relatively wide plate allows for a better observation of the deformation of the wave as it passes over the plate. The speed of the main soliton decreases as the wave propagates over the plate, and it increases as the wave travels from the top of the plate to the deeper water downwave. Farther downwave, the main wave keeps the form of a soliton, while a train of oscillatory waves with smaller wave height (and propagation speed) follows the soliton. Also shown in the figure is the reflection of the waves, both from the leading and trailing edges of the plate. The reflected waves change speed as they travel over the plate back into deeper water.